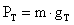Conceptos de Física
El concepto físico de trabajo difiere fundamentalmente de la idea común que de el se tiene. En el lenguaje popular o corriente la expresión trabajo se aplica a cualquier esfuerzo físico o mental que se hace en orden a producir un determinado resultado. así por ejemplo, cuando una persona intenta levantar una piedra sin lograrlo, se dice que ha trabajado mucho y a los estudiantes se les oye decir: me costo mucho trabajo leer la lección de geografía.
En toda idea de trabajo intervienen siempre como elementos una fuerza, un cuerpo, o punto material a que se aplica y un efecto obtenido que se manifiesta por un desplazamiento del punto o cuerpo en la dirección de la fuerza aplicada; son efectos de trabajo mecánico: empujar una nevera para cambiarla de sitio, levantar un ladrillo para colocarlo sobre una mesa, arrastrar una caja, etc...
en cada uno de los anteriores ejemplos hay que fijarse en dos cosas primero, que la persona que realiza el trabajo ejerce una fuerza; de conformidad con lo expuesto, el trabajo podría definirse como: el esfuerzo producido por una fuerza, cuando se mueve en el punto material a que se aplica en la dirección de ella.
Trabajo = fuerza X distancia
W = F . s
La ecuación dimensional del trabajo será pues:
M . L . L
W = = ML²-²
T²
UNIDADES DE TRABAJO
Sistema C.G.S.................................................................... Ergio
Sistema M.K.S.................................................................... Julio
En el valor de trabajo mecánico realizado por el Hombre o por una maquina, el factor tiempo no tiene ninguna influencia, o sea que el trabajo que el trabajo es independiente del tiempo empleado para efectuarlo.
Así por ejemplo, para elevar 200 ladrillos a 5 mts de altura el trabajo que realiza no cambia de valor así se emplee en la mencionada operación dos horas dos días o dos meses. Sin embargo en la actividad industrial no solo es necesario realizar cierta clase de trabajos, sino que es indispensable tener en cuenta el tiempo durante el cual el trabajo debe ser realizado a quien construye una casa o eleva agua con una bomba, no solo le interesa efectuar el trabajo propiamente enunciado, sino que es indispensable tener en cuenta el tiempo durante el cual el tiempo debe ser terminado.
Si dos personas o maquinas realizan el mismo trabajo ( elevar 200 litros de agua a 10 mts de altura ) empleando cada una de ellas diferente tiempo, física mente se le califica diciendo que tienen distancia potencia; si por ejemplo si una persona emplea la mencionada operación dos horas y la otra cinco horas , la primera tiene mayor potencia que la segunda.
Noción. levantar un Kg. del suelo a la mesa, es trabajo que puede hacer un hombre en un segundo, y una hormiga en varias horas por esto es que se dice que el hombre tiene mas fuerza que una hormiga.
POTENCIA = P =
TIEMPO t
F . s
COMO W = F . s P =
T
UNIDADES DE POTENCIA
Siendo la potencia, el trabajo realizado en la unidad de tiempo, se tendrán como sus unidades.
Sistema C.G.S. ................................................................. ergio/seg
Sistema M.K.S. ................................................... .julio/seg = watio
Como unidades secundarias de potencia, se emplean:
kilogrametro/segundo ......................................... kmg/seg
El HP ..................................................................... 75 kgm/seg
El kilo-watt.......................................................... 1000 watios
Se entiende por energía la capacidad que tiene un cuerpo para realizar un trabajo. Como consecuencia de este concepto la energía de un cuerpo o sistema se mide por el trabajo que el cuerpo o sistema realice. La energía que es una puede presentarse bajo diferentes formas como: energía química, luminosa, sonora, mecánica, radiante, nuclear, etc...
El análisis de la energía ha sido uno de los temas mas apasionantes en la evolución de la ciencia, ya que ningún problema de la física puede desligarse de ella.
Definición. La palabra energía representa a todo lo que es trabajo, o que puede convertirse en trabajo. Un cuerpo, o un sistema de cuerpos posee energía cuando es capaz de desarrollar algún trabajo.
Se divide la energía en actual y potencial. Energía actual es la que de hecho aparece como trabajo. Tal es la del agua que mueve una turbina; o la de una bomba que estalla. Energía potencial es la que no se esta convirtiendo en trabajo real, pero puede convertirse en el ; como la de un resorte comprimido, la de una nube electrizada; o la del agua en una represa.
Como formas de energía mecánica, que es nuestro punto directo a estudiar, se conocen:
- Energía cinética
- Energía potencial
Energía cinética: es la capacidad que poseen los cuerpos en movimiento para producir un trabajo; como ejemplos de esta clase de energía podemos citar. corriente de agua o aire, proyectil disparado, tren en marcha, ciclistas en carrera, etc...
En todos estos ejemplos citados, los cuerpos se encuentran en movimiento y con capacidad sobrada para realizar un trabajo.
Nuestra definición de trabajo como la fuerza multiplicada por la distancia ha sido ideada para que concuerde con el concepto de que cantidades iguales de combustible suministraran cantidades iguales de energía. ¿Nos permitirá esta definición del trabajo expresar cuanta energía posee un cuerpo en movimiento? El valor de nuestra definición de trabajo depende de las respuestas que demos a preguntas como esta.
Energía potencial: es la capacidad que tienen los cuerpos para producir un trabajo, en virtud de su forma o de la posición que ocupan. Un cuerpo que se encuentra a cierta altura (martillo) y se deja caer, es capaz de realizar un trabajo, como por ejemplo clavar una estaca. Los grandes depósitos de agua situados a considerable altura (represa) son una verdadera fuente de energía potencial;
en efecto si el agua se conduce por tuberías adecuadas es posible activar turbinas que permitirán la realización de grandes trabajos.
Durante la colisión, la energía cinética total disminuye primero y luego aumenta en las etapas intermedias ha desaparecido parte de la energía cinética.